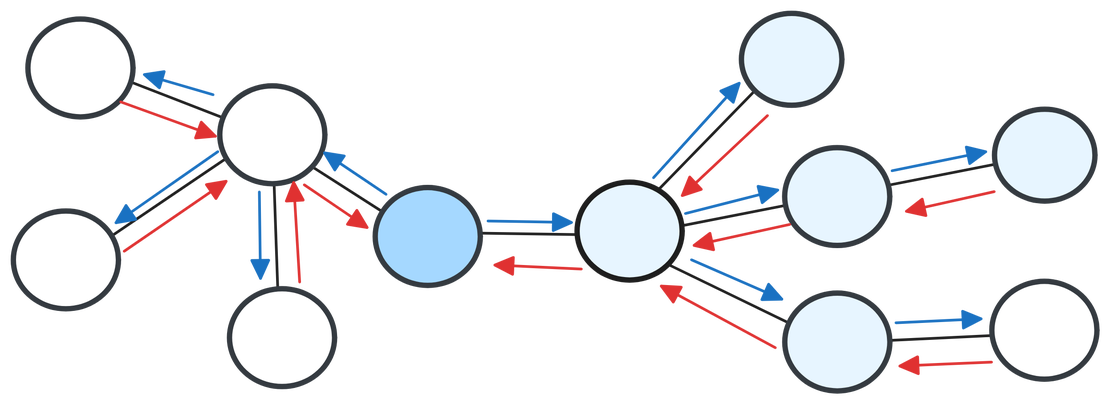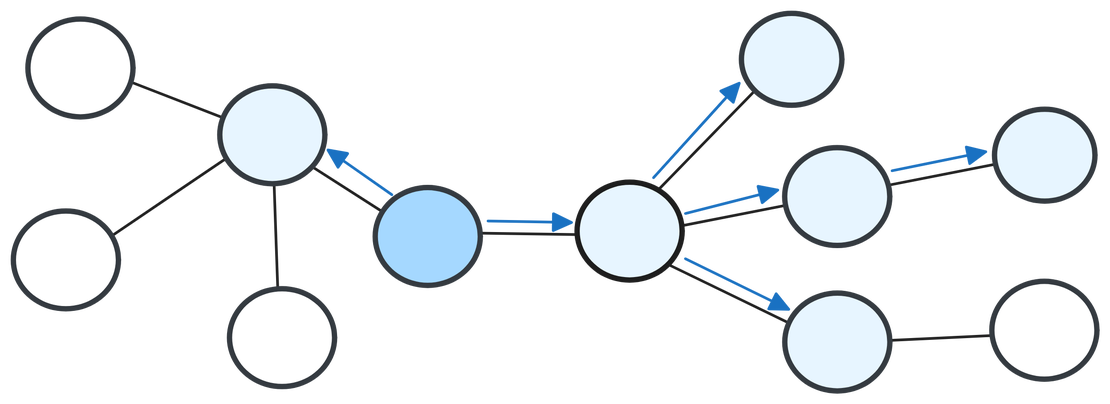
Breadth-First Search (BFS) Algorithm

Introduction

Breadth-First Search (BFS) is one of the fundamental graph traversal algorithms used in computer science. It is particularly effective for searching or traversing tree or graph data structures, exploring nodes level by level from a starting point. BFS is commonly used in scenarios such as finding the shortest path in unweighted graphs, peer-to-peer networks, web crawlers, and more.

BFS Algorithm Step by Step

1. Initialization:

   • Start with a queue (FIFO) and a set or array to track visited nodes.
   • Enqueue the starting node and mark it as visited.

2. Traversal:

   • While the queue is not empty:

     • Dequeue a node from the front.
     • Process the current node.
     • Enqueue all its adjacent nodes that have not been visited.
     • Mark each newly enqueued node as visited.

3. Termination:

   • The algorithm stops when all reachable nodes have been visited and the queue is empty.

Pseudocode

BFS(Graph, start_node):
    create a queue Q
    create a set visited
    enqueue start_node into Q
    add start_node to visited

    while Q is not empty:
        current = Q.dequeue()
        process(current)

        for each neighbor in Graph.adjacent(current):
            if neighbor not in visited:
                Q.enqueue(neighbor)
                visited.add(neighbor)

Time and Space Complexity

Let \(V\) be the number of vertices and \(E\) be the number of edges in the graph.

• Time Complexity: \(\mathcal{O}(V + E)\) because each vertex and edge is processed once.
• Space Complexity: \(\mathcal{O}(V)\) to store visited nodes and the queue.

BFS Example Implementations

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    visited.add(start)

    while queue:
        vertex = queue.popleft()
        print(vertex)

        for neighbor in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

import java.util.*;

public class BFS {
    public static void bfs(Map<String, List<String>> graph, String start) {
        Set<String> visited = new HashSet<>();
        Queue<String> queue = new LinkedList<>();

        queue.add(start);
        visited.add(start);

        while (!queue.isEmpty()) {
            String vertex = queue.poll();
            System.out.println(vertex);

            for (String neighbor : graph.get(vertex)) {
                if (!visited.contains(neighbor)) {
                    visited.add(neighbor);
                    queue.add(neighbor);
                }
            }
        }
    }
}

function bfs(graph, start) {
    let visited = new Set();
    let queue = [start];

    visited.add(start);

    while (queue.length > 0) {
        let vertex = queue.shift();
        console.log(vertex);

        for (let neighbor of graph[vertex]) {
            if (!visited.has(neighbor)) {
                visited.add(neighbor);
                queue.push(neighbor);
            }
        }
    }
}

Related Algorithms

• Depth-First Search (DFS): Explores as far as possible along each branch before backtracking.
• Dijkstra’s Algorithm: Used for shortest path finding in weighted graphs.
• A* Search Algorithm: Heuristic-based pathfinding algorithm.
• Iterative Deepening DFS: Combines the benefits of BFS and DFS.

Limitations

• BFS can be memory intensive due to the queue storing many nodes, especially in wide graphs.
• It may not be optimal in weighted graphs without modification (e.g., use of Dijkstra’s instead).
• Not suitable for infinite or very large graphs without constraints.

Scientific References

1. Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms (3rd ed.). MIT Press.
2. Aho, A. V., Hopcroft, J. E., & Ullman, J. D. (1983). Data Structures and Algorithms. Addison-Wesley.
3. Sedgewick, R., & Wayne, K. (2011). Algorithms (4th ed.). Addison-Wesley.
4. Knuth, D. E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd ed.). Addison-Wesley.