Bellman-Ford Algorithm for Shortest Path

Introduction

The Bellman-Ford algorithm is a fundamental single-source shortest path algorithm used in graph theory. Unlike Dijkstra’s algorithm, Bellman-Ford can handle graphs with negative weight edges, making it versatile for a broader class of problems. It was first proposed by Richard Bellman and Lester Ford in 1958.

📚 Step-by-Step Explanation of the Algorithm

Bellman-Ford works by relaxing all edges repeatedly to find the shortest path from the source vertex to all other vertices in the graph.

🔁 Algorithm Steps:

1. Initialize distances: Set the distance to the source vertex as 0 and all other vertices as infinity.
2. Relax edges repeatedly: For all edges \(V - 1\) times, update the distance if a shorter path is found.
3. Check for negative weight cycles: Iterate through all edges once more to detect any negative cycles.

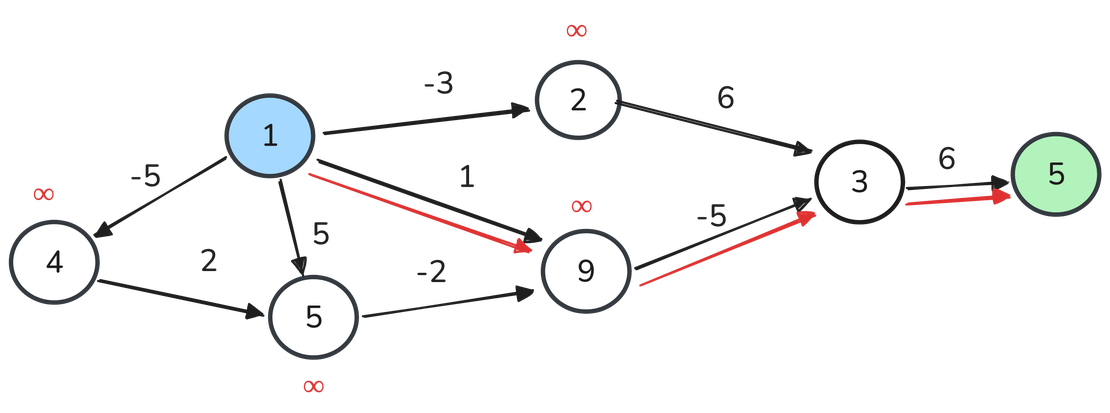
🧮 Illustration:

Graph:
   A ---5---> B
   |         |
  -2         3
   |         v
   C <-------

Step 1: Initialize dist[A] = 0, dist[B] = ∞, dist[C] = ∞

Step 2: Relax all edges:
  A -> B (dist[B] = min(∞, 0 + 5) = 5)
  A -> C (dist[C] = min(∞, 0 - 2) = -2)
  B -> C (dist[C] = min(-2, 5 + 3) = -2)

Step 3: Repeat step 2 for V-1 times

Step 4: Check for negative cycles

⏱️ Time and Space Complexity

• Time Complexity: \(\mathcal{O}(V \cdot E)\)
• Space Complexity: \(\mathcal{O}(V)\) for storing distances

📄 Pseudocode

function BellmanFord(Graph, source):
    initialize distance[] = ∞ for each vertex
    distance[source] = 0

    for i from 1 to V-1:
        for each edge (u, v) with weight w:
            if distance[u] + w < distance[v]:
                distance[v] = distance[u] + w

    for each edge (u, v) with weight w:
        if distance[u] + w < distance[v]:
            report "Negative weight cycle detected"

💻 Implementations

def bellman_ford(edges, V, source):
    dist = [float('inf')] * V
    dist[source] = 0

    for _ in range(V - 1):
        for u, v, w in edges:
            if dist[u] + w < dist[v]:
                dist[v] = dist[u] + w

    for u, v, w in edges:
        if dist[u] + w < dist[v]:
            print("Negative weight cycle detected")

    return dist

class Edge {
    int src, dest, weight;
    Edge(int u, int v, int w) { src = u; dest = v; weight = w; }
}

void bellmanFord(List<Edge> edges, int V, int src) {
    int[] dist = new int[V];
    Arrays.fill(dist, Integer.MAX_VALUE);
    dist[src] = 0;

    for (int i = 1; i < V; ++i) {
        for (Edge edge : edges) {
            if (dist[edge.src] != Integer.MAX_VALUE &&
                dist[edge.src] + edge.weight < dist[edge.dest]) {
                dist[edge.dest] = dist[edge.src] + edge.weight;
            }
        }
    }

    for (Edge edge : edges) {
        if (dist[edge.src] != Integer.MAX_VALUE &&
            dist[edge.src] + edge.weight < dist[edge.dest]) {
            System.out.println("Graph contains a negative weight cycle");
        }
    }
}

function bellmanFord(edges, V, source) {
    let dist = Array(V).fill(Infinity);
    dist[source] = 0;

    for (let i = 0; i < V - 1; i++) {
        for (let [u, v, w] of edges) {
            if (dist[u] + w < dist[v]) {
                dist[v] = dist[u] + w;
            }
        }
    }

    for (let [u, v, w] of edges) {
        if (dist[u] + w < dist[v]) {
            console.log("Negative weight cycle detected");
        }
    }
    return dist;
}

🌍 Real-World Applications

• Routing algorithms in computer networks (e.g., RIP protocol)
• Currency arbitrage detection in financial systems
• Project scheduling with time constraints and costs
• Traffic navigation when delays (positive or negative) can be incurred

🔗 Related Algorithms

• Dijkstra’s Algorithm: Faster but cannot handle negative weights.
• Floyd-Warshall Algorithm: All-pairs shortest paths, \(\mathcal{O}(V^3)\).
• A Search*: Heuristic-based pathfinding.
• Johnson’s Algorithm: All-pairs shortest path in sparse graphs with negative weights.

⚠️ Limitations of Bellman-Ford

• Slower than Dijkstra for dense graphs: \(\mathcal{O}(V \cdot E)\)
• Detects but does not recover negative cycles.
• Does not scale well for very large graphs.

📖 Scientific References

• Bellman, R. (1958). On a Routing Problem. Quarterly of Applied Mathematics.
• Ford, L. R. (1956). Network Flow Theory. RAND Corporation.
• Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms, MIT Press.
• Tarjan, R. E. (1983). Data Structures and Network Algorithms, SIAM.